TRANSFORMACIONES LINEALES ejercicios RESUELTOS paso a paso APLICACIONES LINEALES T(x,y)=(x , y

Clase 17 Álgebra Lineal. Transformaciones Lineales Matriz asociada a una transformación YouTube

Al multiplicar una matriz por un vector, se obtiene el resultado de aplicar la transformación lineal a ese vector. Las transformaciones lineales tienen algunas propiedades importantes: 1. Preservación de la suma: La transformación de la suma de dos vectores es igual a la suma de las transformaciones de los vectores individuales. Es decir, si.

Transformación Lineal. Transformación Lineal Definida por una Matriz Ejercicio. YouTube

Matriz de transformación. Efecto de aplicar varias matrices de transformación afín 2D sobre un cuadrado unitario (de lado 1). Téngase en cuenta que las matrices de reflexión son casos especiales de la matriz de escala. En álgebra lineal, una aplicación lineal se puede representar mediante una matriz. Si es una transformación lineal que.

Matriz asociada a una transformación lineal [Ejemplos y videos]

Se puede recordar de \(\mathbb{R}^n\) que la matriz de una transformación lineal depende de las bases elegidas. Este concepto se explora en esta sección, donde la transformación lineal ahora mapea de un espacio vectorial arbitrario a otro. Dejar \(T: V \mapsto W\) ser un isomorfismo donde \(V\) y \(W\) son espacios vectoriales.

Matriz asociada a una transformación lineal respecto de bases B1 B2 04 YouTube

Encontrar la matriz de una transformación lineal con respecto a la base estándar. Determinar la acción de una transformación lineal sobre un vector en \(\mathbb{R}^n\). En los ejemplos anteriores, la acción de las transformaciones lineales consistió en multiplicarse por una matriz. Resulta que este es siempre el caso de las.

Matriz asociada a una transformación lineal respecto de bases B1 B2 01 YouTube

Transcripción del video. supongamos que tienes una matriz de n por n elementos que se mira algo así tienes en la primera columna el primer elemento de la primera columna es 1 y el resto de los elementos en la columna son ceros entonces tienes 10 y 000 hasta llegar al enésimo término que también es 0 ahora en la en la segunda columna tienes.

Matriz asociada a una transformación lineal respecto de bases B1 B2 03 YouTube

Transcripción del video. en el vídeo pasado definimos lo que era una transformación que era simplemente una función que operaba en vectores ahora vamos a hablar de un caso especial de las transformaciones vamos a hablar de las transformaciones lineales transformaciones lineales después de todo esto es álgebra lineal y ya hemos hablado.

PPT Álgebra de Transformaciones Lineales PowerPoint Presentation, free download ID591839

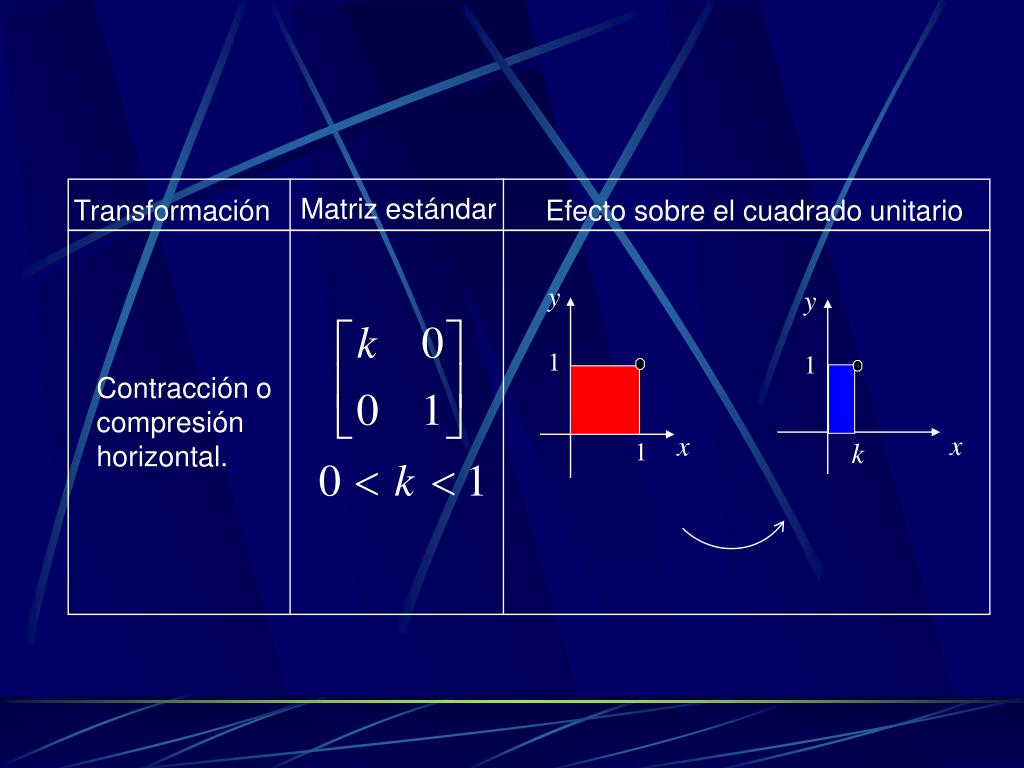
Construcción de la matriz asociada a una transformación lineal. Hemos visto ejemplos de cómo surge a partir del producto de matrices, la matriz estándar de una transformación lineal de \ ( {\mathbb {R}^n}\) a \ ( {\mathbb {R}^m}\). En lo que sigue intentaremos generalizar para cualquier espacio vectorial de dimensión finita, el concepto.

Matriz de una transformación lineal de R3 a R2 YouTube

El rango de una matriz A en M m, n ( F) es el rango de la transformación lineal asociada de F n a F m dada por X ↦ A X. Lo denotamos por rank ( A). A partir de esta definición y de las propiedades de rango para transformaciones lineales obtenemos directamente las siguientes propiedades para rango de matrices.

200502 Matriz de una transformacion lineal e isomorfismos YouTube

Para aquellos de ustedes aficionados a la terminología elegante, estas acciones animadas pueden describirse como "transformaciones lineales del espacio unidimensional".La palabra "transformación" tiene el mismo significado que la palabra "función": algo que toma un número y devuelve otro, por ejemplo f (x) = 2 x ‍ .Sin embargo, mientras que típicamente visualizamos las funciones con.

Matriz asociada a una transformacion lineal

Ejemplos de transformaciones lineales: reflejar y escalar. Ejemplos de transformaciones lineales: rotar en R2. Rotación alrededor del eje x en R3. Vectores unitarios. Introducción a las proyecciones. Expresar una proyección en una recta como un producto de matrices y vectores.

MATRIZ ASOCIADA A UNA TRANSFORMACION LINEAL YouTube

Utilizar propiedades de transformaciones lineales para resolver problemas. Encontrar el compuesto de transformaciones y el inverso de una transformación. Dejar \ (T: \mathbb {R}^n \mapsto \mathbb {R}^m\) ser una transformación lineal. Después hay algunas propiedades importantes de las \ (T\) cuales serán examinadas en esta sección.

5.3 Representacion Matricial de una Transformación Lineal

Una matriz asociada a una transformación lineal es una representación algebraica de dicha transformación. Esta matriz nos permite realizar cálculos y manipulaciones matemáticas con mayor facilidad. Además, nos brinda una forma visual de comprender cómo la transformación afecta a los vectores en el espacio.

Matriz asociada a una transformación lineal respecto de bases B1 B2 02 YouTube

Una matriz de la transformación lineal es una matriz que representa la transformación lineal en términos de las coordenadas de los vectores. Para entender cómo se construye esta matriz, consideremos un ejemplo concreto. Supongamos que tenemos una transformación lineal T que mapea un vector de un espacio vectorial de dimensión n a otro.

Representación Matricial de una Transformación lineal YouTube

Para calcular la matriz de una transformación lineal, debemos seguir los siguientes pasos: 1. Escoger una base para el espacio vectorial de entrada y otra para el espacio vectorial de salida. Una base es un conjunto de vectores linealmente independientes que generan el espacio vectorial. 2.

Matriz asociada a una transformacion lineal

No todas las matrices de 3x3 dan transformaciones biyectivas de R3, la transformación es biyectiva si tiene una inversa. Por el lema anterior, si la transformación T está dada por la matriz M, entonces la inversa de T esta dada por la matriz inversa M-1 Ejemplo. La inversa de la transformación T(x,y,z)=(x,x+y,x+y+z) es T -1(x,y,z)=(x,y-x,z.

La Matriz de una Transformación Lineal YouTube

This page titled 5.8: La Matriz de una Transformación Lineal II is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Ken Kuttler via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.